一枚の面で光を集める

高２の生徒に物理の波動あたりを教えなければいけないということで，なぜかファインマン物理学Ⅱを読んでいる今日このごろ．波動は大学入ってからしっかり勉強していないからこの機会に読み切りたいところだけど．

やっぱりファインマン物理学はおもしろくて，P.14に
「一枚の屈折面で，その両側の屈折率が違っているとする．左側の光の速さが１，右側で1/nになるとしよう．このとき屈折面より左側の点Oから出た光が，屈折したあとに必ずある点O'を通るような屈折面の形（複雑な４次関数になる．）を求めてみよ．」
的なことが書いてある．これどんな形状か気になるからやってみよう．

まず問題の設定から

上図のように記号と座標を設定．実際にグラフを描きたいので，n=2，x0=-1，x0'=1とすると，点Pの場所によらずかかる時間が同じで（まっすぐいったときと同じ）あるための条件は

これに上の具体的な数字を代入してルートをはずしていくと

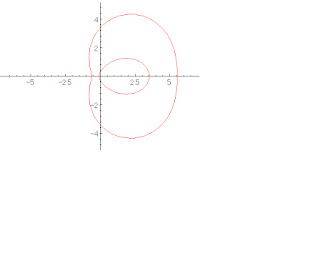
となり，陰関数表示が得られる．これをグラフにかくと

となる．
内側の曲線を（または外側の曲線）ふちとするガラスをおいてあげると，集光される．

またn=3,x0'=3とすると，

 てな感じ

おまけ
GCalc-Plusというソフトウェアを使って陰関数のグラフを作成しました．（だから正直正しいか，どのくらい誤差あるかとかわからないです．）無料ソフトウェアですが，使いかってがとてもよかったです．